The Problem With “Total Clutch” Hitting Statistics

 

by Cyril Morong

Email

Click here to see my sabermetric blog called Cybermetrics

 

 

 

Introduction

 

A recent article (late 2003) appeared in BusinessWeek magazine called “Ball Park Figures You Can Bet On” which described a “new statistic” developed by Benjamin Polak and Brian Lonergan of Yale University which measures “wins contributed” by major league hitters. (another article on their work appeared in Nov. 2004 in the NY Times-see sources below) From the online version:

 

“Here's how their method works: Let's say the home team is down by two runs in the bottom of the fifth inning, with no outs and a runner on second base. At that moment, the home team has a 39% chance (or 0.39 probability) that it will win. If the batter grounds out, and the runner at second fails to advance, the team's chance of winning falls to 33%. The difference between the two, -0.06, is assigned to the batter who just grounded out.”

 

Now they add this up for the whole season, every plate appearance and get wins contributed for each player (see link in sources).

 

The problem with this approach is that it is not new and that it really tells us nothing about what a ball player is worth since in the long run this “total clutch” stat is highly correlated with normal hitting statistics, as I will demonstrate(my critique is not new-See the book "The Hidden Game of Baseball" by John Thorn and Pete Palmer. They discuss what Dick Cramer had to say about the Mills brothers)  By “total clutch” stat, I mean one that takes into account every plate appearance and each one is weighted by its importance according to the score and inning.  Hits when the game is late and close will count for more than hits when the game is early and the score is lopsided.

 

History

 

This is definitely not a new stat.  It goes back at least as far as 1970 when Eldon G. and Harlan D. Mills published their book Player Win Averages.  Polak and Lonergan’s “wins contributed” stat is similar. So is the “Player Game Percentage” in the book Curve Ball by Jim Albert and Jay Bennett.  So is the “Game State Victories (or Wins) found at the Rhoids Sports Analysis website (see sources).  So is “player's win value” by Ed Oswalt (his link is also in sources).  So what Lonergan and Polak have done is definitely not new.

 

Analysis

 

Let’s start with the Ed Oswalt’s measure “player’s win value” (or PWV) since he uses thirty years of data, covering the years 1972-2002. The best hitters on his list will not surprise you and his stat divided by plate appearances (or PA) is highly correlated with stats like on-base percentage (OBP) and slugging percentage (SLG) as well as OPS (OBP + SLG).

 

First, I looked at the top 100 players in plate appearances from 1972-2002.  I then correlated relative OPS (relative to the league average for each player) with Oswalt’s PWV/PA.  The correlation was 0.948.  This is very close to a one-to-one relationship.  If you square this (called r-squared), you get 0.898, meaning that 89.8% of the variation across hitters in PWV/PA is explained by relative OPS.  This is important because it shows that a very simple, non-clutch, non-situational, non-context stat like OPS pretty much explains a much more complex context dependent stat that is supposed to tell us the value of hitters.

 

The linear regression equation is PWV/PA = .00022*OPS - 022

 

In the figure below, you can see the relationship where PWV/PA is a function of relative OPS.

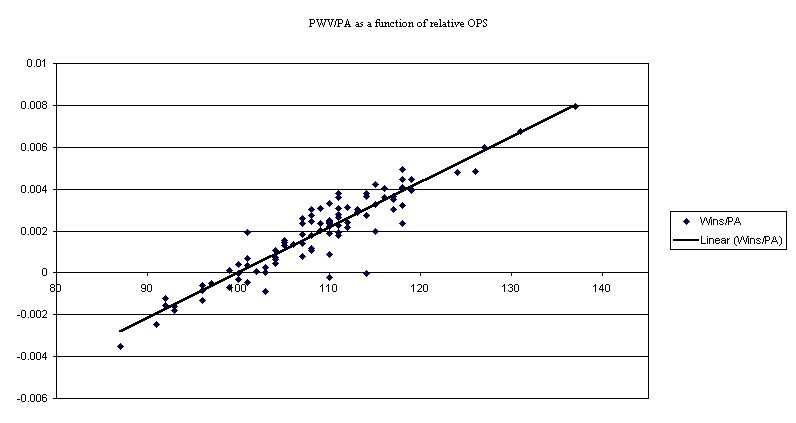
In the table below, you can see each player’s PWV/PA and his relative OPS.  Bonds, for example has 137, which means his OPS was 37% higher than the league average for the 1972-2002 period.  The top ten or twenty hitters will not surprise you.

 

Rank	Player	PWV/PA	Relative OPS
1	Barry Bonds	0.0080	137
2	Mark McGwire	0.0068	131
3	Jeff Bagwell	0.0060	127
4	Will Clark	0.0050	118
5	Mike Schmidt	0.0049	126
6	Ken Griffey Jr.	0.0048	124
7	George Brett	0.0045	119
8	Rod Carew	0.0045	118
9	Tony Gwynn	0.0042	115
10	Jack Clark	0.0041	118
11	Reggie Jackson	0.0040	118
12	John Olerud	0.0040	116
13	Fred McGriff	0.0040	119
14	Rafael Palmeiro	0.0039	119
15	Kirby Puckett	0.0038	114
16	Mark Grace	0.0038	111
17	Rickey Henderson	0.0038	114
18	Eddie Murray	0.0037	114
19	Dwight Evans	0.0037	117
20	Wade Boggs	0.0036	116
21	Ken Singleton	0.0036	111
22	Keith Hernandez	0.0036	110
23	Fred Lynn	0.0035	117
24	Darrell Evans	0.0033	110
25	Jose Canseco	0.0033	115
26	Jim Rice	0.0032	118
27	Dave Parker	0.0031	112
28	Harold Baines	0.0031	111
29	Ken Griffey Sr.	0.0031	109
30	Don Mattingly	0.0030	113
31	Toby Harrah	0.0030	108
32	Ellis Burks	0.0030	117
33	Andres Galarraga	0.0029	113
34	Tim Raines	0.0028	111
35	Lou Whitaker	0.0027	108
36	Dave Winfield	0.0027	114
37	Cecil Cooper	0.0026	111
38	Pete Rose	0.0026	107
39	Paul Molitor	0.0025	110
40	Gary Matthews	0.0025	108
41	Ted Simmons	0.0025	110
42	Dale Murphy	0.0024	114
43	Al Oliver	0.0024	112
44	Roberto Alomar	0.0024	110
45	Brian Downing	0.0024	110
46	Jose Cruz	0.0024	107
47	Craig Biggio	0.0023	110
48	Dusty Baker	0.0023	109
49	Sammy Sosa	0.0023	118
50	Wally Joyner	0.0023	111
51	Paul O'Neill	0.0022	111
52	Barry Larkin	0.0022	110
53	Bobby Grich	0.0021	112
54	Steve Garvey	0.0020	109
55	Bobby Bonilla	0.0020	115
56	Ron Cey	0.0019	111
57	Tony Phillips	0.0019	101
58	Carlton Fisk	0.0019	111
59	Ryne Sandberg	0.0019	110
60	Robin Ventura	0.0018	107
61	Andre Dawson	0.0018	111
62	Chili Davis	0.0018	108
63	Alan Trammell	0.0016	105
64	Chris Chambliss	0.0014	105
65	Robin Yount	0.0014	107
66	Cal Ripken	0.0014	106
67	Julio Franco	0.0013	106
68	Graig Nettles	0.0013	105
69	George Hendrick	0.0012	108
70	Brett Butler	0.0011	104
71	Don Baylor	0.0011	108
72	Chet Lemon	0.0009	110
73	Gary Carter	0.0008	107
74	Brady Anderson	0.0008	104
75	Bill Buckner	0.0007	101
76	Ruben Sierra	0.0007	104
77	Carney Lansford	0.0007	104
78	Buddy Bell	0.0004	104
79	Joe Carter	0.0004	104
80	Willie Randolph	0.0004	100
81	Tony Fernandez	0.0004	101
82	Todd Zeile	0.0003	103
83	B.J. Surhoff	0.0001	99
84	Jay Bell	0.0001	102
85	Steve Finley	0.0000	103
86	Willie McGee	0.0000	100
87	Gary Gaetti	-0.0003	100
88	Tim Wallach	-0.0005	101
89	Terry Pendleton	-0.0005	97
90	Dave Concepcion	-0.0006	96
91	Devon White	-0.0007	99
92	Steve Sax	-0.0009	96
93	Lance Parrish	-0.0009	103
94	Omar Vizquel	-0.0012	92
95	Willie Wilson	-0.0013	96
96	Ozzie Smith	-0.0015	92
97	Garry Templeton	-0.0016	93
98	Frank White	-0.0018	93
99	Bob Boone	-0.0025	91
100	Larry Bowa	-0.0035	87

 

 

I then ran a linear regression in which PWV/PA was the dependent variable and relative OBP and SLG were the independent variables. It used all 284 players with 5000 or more plate appearances from 1972-2002.  The regression equation was

 

PWV/PA = -.0246 + .000149*OBP + .000097*SLG

 

The r-squared was .935, meaning that 93.5% of the variation in PWV/PA is explained by the model.  The standard error is .00056 or about .39 wins for a 700 PA season.  The correlation between OBP and SLG is about .52.  Each of those has a correlation of over .8 with Wins/PA. So again, two very simple stats explain what is going on with the much more complex, clutch stat.

 

To see how each player did compared to what the above equation predicted, go to the following link. You can also see which hitters exceeded their predicted PWV/PA the most.

 

How Many Games Do Clutch Hitters Really Win?

 

Now another stat, the Game State Victories (GSV) from the Rhoids Sports Analysis website, shows the same tendencies.

 

I have a data set with 191 players who have 900 or more at bats over the years 2001-2003. (this is not all of them-I'll explain later).  So I ran a regression in which each hitter's GSV for the three seasons was the dependent variable and their cumulative totals for various other stats were the independent variables.  The r-squared I got was .91, meaning that 91% of the variation in GSV across hitters is explained by regular counting stats that are not at all context dependent (well, not quite, again I will explain later-it concerns SACs).  That is, these independent variables have nothing to do with the score or the inning.  Yet they explain almost all of the variation in the context dependent variable.

 

Here are the coefficient estimates

 

SAC = -.021

SF = -.049

GIDP = -.1098

CS = -.059

SB = .0299

BB = .053

HR = .106

3B = .099

2B = .0877

1B = .0603

OUTS = -.01537

Intercept = -1.47

 

Outs means outs not counting the GIDP. BB includes hit by pitch.  The only variables not statistically significant (T-value less than 1.96) are SAC, SF and CS. That is a surprise for CS.   I believe that GSV or anything like it is a clutch stat.  Yet non-clutch data does a very good job of explaining the variation in GSV. It is possible that the unexplained variation is due to chance and not any kind of clutch hitting ability.

 

Now the data.  I chose 900 at-bats because the data given that I was able to download from the Rhoids website, listed other stats, but not walks.  So I wanted a convenient cutoff for which players to count and I chose 300 for individual years, figuring anyone who gets 400 plate appearances probably has at least 300 at bats.  And over three years that is 900. I also used the data from Doug Steele's website to get walks, GIDP, etc.

 

The data problems.  In some years, players who obviously did very well had zero for their GSV.  Very often they were rookies who also had a zero listed for their salary and the Rhoids people wanted to do something with runs per dollar.  Maybe that is why a zero is given, since you cannot divide by zero. Also some players simply had an "NA" listed.  Others clearly had the wrong number, like Juan Sosa getting the same GSV as Sammy Sosa one year.  Some other players were just not listed.  I did not see Edgar Martinez in the "data dump" for this year.  I could not always tell which Alex Gonzalez I was looking at or if I did they were not listed for all years.  Some player names were not spelled the same way each year (I went through and made the necessary corrections to allow for doing subtotals in excel).  So I did not have all of the players with 900 or more at bats from this period.  I think about 30 got left out. 

 

The correlation between GSV per plate appearance for players with 300 or more at bats in both 2001 and 2002 was .5.  But the correlation between OPS in 2001 and GSV per PA in 2002 was actually higher, at .519.  So if you wanted to predict a player's GSV per PA in 2002, his OPS in 2001 would do a slightly better job than his GSV per PA in 2001.

 

I also calculated a predicted GSV per PA for these players in both 2001 and 2002 using the coefficient values from the regression which used 1Bs, 2Bs, 3Bs, HRs, BBs, SBs, CSs, Outs and GIDPs. Then I calculated the difference between the actual GSV per PA in each year and the predicted GSV per PA in each year.  Then I found the correlation between the differences or residuals for the two years and it was .081.  That seems very low. I think this means that players who were especially good in the clutch in 2001 (who had a higher GSV per PA than predicted) were not likely to again, in 2002, have a higher GSV per PA than predicted in 2002 (I think this is the kind of analysis that Dick Cramer performed on the Player Win Average of the Mills brothers).

 

 

Sources

 

"Ballpark Figures to Bet On," Nov. 21, UPFRONT section BusinessWeek magazine. Author was Brian Hindo.

 

“What's a Ball Player Worth?” can be found at:

 

http://www.businessweek.com/print/bwdaily/dnflash/nov2003/nf2003115_2313_db016.htm?db

 

Player Win Averages by Eldon G. and Harlan D. Mills.  1970. A.S. Barnes, publisher.

 

Curve Ball: Baseball, Statistics, and the Role of Chance in the Game by Jim Albert and Jay Bennett. Revised 2003. Copernicus Books.

 

Rhoids Sports Analysis: http://www.rhoids.com/

 

Ed Oswalt’s site is at: http://www.livewild.org/bb/playervalues/index.html

 

 

The Nov. 7, 2004 NY Times article is at

 

http://query.nytimes.com/gst/abstract.html?res=F30A1EFA39580C748CDDA80994DC404482

 

But you will probably have to pay to read all of it.

 

Other sites where you might find it are

 

http://www.iht.com/articles/2004/11/07/sports/base.html

 

http://redsox.mostvaluablenetwork.com/wp-content/sites/schwarzWRAP.html